Algebra de boole

ÁLGEBRA DE BOOLE

Álgebra de Boole también llamada álgebra booleana, en informática y matemática es una estructura algebraica que esquematiza las operaciones lógicas.

Historia

Se denomina así en honor a George Boole (2 de noviembre de 1815 a 8 de diciembre de 1864), matemático inglés autodidacta, que fue el primero en definirla como parte de un sistema lógico, inicialmente en un pequeño folleto, The Mathematical Analysis of Logic,¹​ publicado en 1847, en respuesta a una controversia en curso entre Augustus De Morgan y sir William Rowan Hamilton. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional. Más tarde fue extendido como un libro más importante: An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities (también conocido como An Investigation of the Laws of Thought²​ o simplemente The Laws of Thought³​), publicado en 1854.

Las interpretaciones respectivas de los símbolos 0 y 1 en el sistema de lógica son Nada y Universo.

George Boole⁴​

En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948. Esta lógica se puede aplicar a dos campos:

• Al análisis, porque es una forma concreta de describir como funcionan los circuitos.
• Al diseño, ya que teniendo una función aplicamos dicha álgebra, para poder desarrollar una implementación de la función.

Definición

Dado un conjunto ${\displaystyle {\mathfrak {B}}}$ en el que se han definido dos leyes de composición interna ${\displaystyle \oplus ,\odot }$. La estructura ${\displaystyle ({\mathfrak {B}},\oplus ,\odot )}$ es un álgebra de Boole si y solo si ${\displaystyle ({\mathfrak {B}},\oplus ,\odot )}$es un Retículo distributivo,⁵​ esto es:

• ${\displaystyle \odot }$ es distributiva respecto a ${\displaystyle \oplus }$:

${\displaystyle a\odot (b\oplus c)=(a\odot b)\oplus (a\odot c)}$

• ${\displaystyle \oplus }$ es distributiva respecto a ${\displaystyle \odot }$

${\displaystyle a\oplus (b\odot c)=(a\oplus b)\odot (a\oplus c)}$

Basándose en esta definición se determina lo siguiente.

Principio

Dado un conjunto: ${\displaystyle {\mathfrak {B}}}$ formado cuando menos por los elementos: ${\displaystyle \varnothing ,\;U}$ en el que se ha definido:

• Una operación unaria interna, que llamaremos complemento:

${\displaystyle {\begin{array}{rrcl}\sim :&{\mathfrak {B}}&\to &{\mathfrak {B}}\\&a&\to &b=\sim a\end{array}}}$

En esta operación definimos una aplicación que, a cada elemento a de B, le asigna un b de B.

${\displaystyle \forall a\in {\mathfrak {B}}\,:\quad \exists !b\in {\mathfrak {B}}\;/\quad b=\sim a}$

Para todo elemento a en B, se cumple que existe un único b en B, tal que b es el complemento de a.

• La operación binaria interna, que llamaremos suma:

${\displaystyle {\begin{array}{rrcl}\oplus :&{\mathfrak {B}}\times {\mathfrak {B}}&\to &{\mathfrak {B}}\\&(a,b)&\to &c=a\oplus b\end{array}}}$

por la que definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.

${\displaystyle \forall (a,b)\in {\mathfrak {B}}\times {\mathfrak {B}}\,:\quad \exists !c\in {\mathfrak {B}}\;/\quad c=a\oplus b}$

Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de sumar a con b.

• La operación binaria interna, que llamaremos producto:

${\displaystyle {\begin{array}{rrcl}\odot :&{\mathfrak {B}}\times {\mathfrak {B}}&\to &{\mathfrak {B}}\\&(a,b)&\to &c=a\odot b\end{array}}}$

Con lo que definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.

${\displaystyle \forall (a,b)\in {\mathfrak {B}}\times {\mathfrak {B}}\,:\quad \exists !c\in {\mathfrak {B}}\;/\quad c=a\odot b}$

Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado del producto a y b.

Dada la definición del álgebra de Boole como una estructura algebraica genérica, según el caso concreto de que se trate, la simbología y los nombres de las operaciones pueden variar.

Axiomas necesarios

Diremos que este conjunto y las operaciones así definidas: ${\displaystyle ({\mathfrak {B}},\sim ,\oplus ,\odot )}$ son un álgebra de boole, si cumple las siguientes axiomas:

• 1a: La ley asociativa de la suma:

${\displaystyle \forall a,b,c\in {\mathfrak {B}}:\;(a\oplus b)\oplus c=a\oplus (b\oplus c)}$

• 1b: La ley asociativa del producto:

${\displaystyle \forall a,b,c\in {\mathfrak {B}}:\;(a\odot b)\odot c=a\odot (b\odot c)}$

• 2a: Existencia del elemento neutro para la suma:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\oplus \varnothing =a}$

• 2b: Existencia del elemento neutro para el producto:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\odot U=a}$

• 3a: La ley conmutativa de la suma:

${\displaystyle \forall a,b\in {\mathfrak {B}}:\;a\oplus b=b\oplus a}$

• 3b: La ley conmutativa del producto:

${\displaystyle \forall a,b\in {\mathfrak {B}}:\;a\odot b=b\odot a}$

• 4a: Ley distributiva de la suma respecto al producto:

${\displaystyle \forall a,b,c\in {\mathfrak {B}}:\;a\oplus (b\odot c)=(a\oplus b)\odot (a\oplus c)}$

• 4b: Ley distributiva del producto respecto a la suma:

${\displaystyle \forall a,b,c\in {\mathfrak {B}}:\;a\odot (b\oplus c)=(a\odot b)\oplus (a\odot c)}$

• 5a: Existe elemento complemento para la suma:

${\displaystyle \forall a\in {\mathfrak {B}};\;\exists \sim a\in {\mathfrak {B}}:\;a\oplus \sim a=U}$

• 5b: Existe elemento complemento para el producto:

${\displaystyle \forall a\in {\mathfrak {B}};\;\exists \sim a\in {\mathfrak {B}}:\;a\odot \sim a=\varnothing }$

Teoremas fundamentales

Partiendo de los cinco axiomas anteriores, se pueden deducir y demostrar los siguientes teoremas fundamentales:

• Ley de idempotencia para la suma:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\oplus a=a}$

• Ley de idempotencia para el producto:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\odot a=a}$

• Ley de absorción para la suma:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\oplus U=U}$

• Ley de absorción para el producto:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\odot \varnothing =\varnothing }$

• Ley de identidad para la suma:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\oplus \varnothing =a}$

• Ley de identidad para el producto:

${\displaystyle \forall a\in {\mathfrak {B}}:\;a\odot U=a}$

• Ley de involución:

${\displaystyle \forall a\in {\mathfrak {B}}:\;\sim (\sim a)=a}$

• 10: Ley del complemento:

${\displaystyle \sim U=\varnothing }$

${\displaystyle \sim \varnothing =U}$

• 11: Leyes de De Morgan:

${\displaystyle \forall a,b\in {\mathfrak {B}}:\;\sim (a\oplus b)=\sim a\odot \sim b}$

${\displaystyle \forall a,b\in {\mathfrak {B}}:\;\sim (a\odot b)=\sim a\oplus \sim b}$

Orden en el álgebra de Boole

Sea: ${\displaystyle ({\mathfrak {B}},\sim ,\oplus ,\odot )}$ un álgebra de Boole, sean a, b dos elementos del conjunto, podremos decir entonces que a antecede a b y lo denotamos:

${\displaystyle a\preceq b}$

si se cumple alguna de las siguientes condiciones:

1. ${\displaystyle a\oplus b=b}$
2. ${\displaystyle a\odot b=a}$
3. ${\displaystyle \sim a\oplus b=U}$
4. ${\displaystyle a\odot \sim b=\varnothing }$

Estas cuatro condiciones se consideran equivalentes y el cumplimiento de una de ellas implica necesariamente el cumplimiento de las demás. Definiendo un conjunto parcialmente ordenado.

Si se cumple que:

${\displaystyle a,b\in {\mathfrak {B}}\;:\quad a\preceq b\;\lor \;b\preceq a\quad \longrightarrow \quad a,b\rightarrow {\mathit {comparables}}}$

Para los valores a, b de ${\displaystyle {\mathfrak {B}}}$, que cumplen que a antecede a b, o que b antecede a a, se dice que a y b son comparables.

Si se cumple que:

${\displaystyle a,b\in {\mathfrak {B}}\;:\quad a\npreceq b\;\land \;b\npreceq a\quad \longrightarrow \quad a,b\rightarrow {\mathit {no\;comparables}}}$

Para los valores a, b de ${\displaystyle {\mathfrak {B}}}$, que cumplen que a no antecede a b, y que b no antecede a a, se dice que a y b son no comparables.

Principio de dualidad

El concepto de dualidad permite formalizar este hecho: a toda relación o ley lógica le corresponderá su dual, formada mediante el intercambio de los operadores suma con los de producto, y de los ${\displaystyle U\;}$ con los ${\displaystyle \varnothing }$.

	Adición	Producto
1	${\displaystyle a\oplus \sim {a}=U\,}$	${\displaystyle a\odot \sim {a}=\varnothing }$
2	${\displaystyle a\oplus \varnothing =a\,}$	${\displaystyle a\odot U=a\,}$
3	${\displaystyle a\oplus U=U\,}$	${\displaystyle a\odot \varnothing =\varnothing \,}$
4	${\displaystyle a\oplus a=a\,}$	${\displaystyle a\odot a=a\,}$
5	${\displaystyle a\oplus b=b\oplus a\,}$	${\displaystyle a\odot b=b\odot a\,}$
6	${\displaystyle a\oplus (b\oplus c)=(a\oplus b)\oplus c\,}$	${\displaystyle a\odot (b\odot c)=(a\odot b)\odot c\,}$
7	${\displaystyle a\oplus (b\odot c)=(a\oplus b)\odot (a\oplus c)\,}$	${\displaystyle a\odot (b\oplus c)=(a\odot b)\oplus (a\odot c\,)}$
8	${\displaystyle a\oplus a\odot b=a\,}$	${\displaystyle a\odot (a\oplus b)=a\,}$
9	${\displaystyle \sim {(a\oplus b)}=\sim {a}\odot \sim {b}}$	${\displaystyle \sim {(a\odot b)}=\sim {a}\oplus \sim {b}\,}$

Otras formas de notación del álgebra de Boole

En Lógica binaria se suele emplear la notación ${\displaystyle (\{0,1\},{\bar {}},+,\cdot )}$, común en la tecnología digital, siendo la forma más usual y la más cómoda de representar.

Por ejemplo las leyes de De Morgan se representan así:

${\displaystyle {\overline {a+b}}={\bar {a}}\cdot {\bar {b}}\,}$

${\displaystyle {\overline {a\cdot b}}={\bar {a}}+{\bar {b}}\,}$

Cuando el álgebra de Boole se emplea en electrónica, suele emplearse la misma denominación que para las puerta lógica AND (Y), OR (O) y NOT (NO), ampliándose en ocasiones con X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia). las variables pueden representarse con letras mayúsculas o minúsculas, y pueden tomar los valores {0, 1}

Empleando esta notación las leyes de De Morgan se representan:

${\displaystyle {\mbox{NOT }}(a{\mbox{ OR }}b)={\mbox{NOT }}a{\mbox{ AND }}{\mbox{NOT }}b\,}$

${\displaystyle {\mbox{NOT }}(a{\mbox{ AND }}b)={\mbox{NOT }}a{\mbox{ OR }}{\mbox{NOT }}b\,}$

En su aplicación a la lógica se emplea la notación ${\displaystyle \land \lor \lnot }$ y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}

Con la notación lógica las leyes de De Morgan serían así:

${\displaystyle \lnot {(a\lor b)}=\lnot {a}\land \lnot {b}\,}$

${\displaystyle \lnot {(a\land b)}=\lnot {a}\lor \lnot {b}\,}$

En el formato de Teoría de conjuntos el Álgebra de Boole toma el aspecto: ${\displaystyle ({\mathcal {P}}(U),\sim ,\cup ,\cap )}$

En esta notación las leyes de De Morgan serían así:

${\displaystyle \sim {(a\cup b)}=\;\sim {a}\;\cap \sim {b}\,}$

${\displaystyle \sim {(a\cap b)}=\;\sim {a}\;\cup \sim {b}\,}$

Otra forma en la álgebra de conjuntos del Álgebra de Boole, las leyes de De Morgan serían así:

${\displaystyle {(A\cup B)}^{C}=\;{A}^{C}\cap {B}^{C}}$

${\displaystyle {(A\cap B)}^{C}=\;{A}^{C}\cup {B}^{C}}$

Desde el punto de vista práctico existe una forma simplificada de representar expresiones booleanas. Se emplean apóstrofos (') para indicar la negación, la operación suma (+) se representa de la forma normal en álgebra, y para el producto no se emplea ningún signo, las variables se representan, normalmente con una letra mayúscula, la sucesión de dos variables indica el producto entre ellas, no una variable nombrada con dos letras.

La representación de las leyes de De Morgan con este sistema quedaría así, con letra minúsculas para las variables:

${\displaystyle (a+b)'=a'b'\,}$

${\displaystyle (ab)'=a'+b'\,}$

y así, empleando letras mayúsculas para representar las variables:

${\displaystyle (A+B)'=A'B'\,}$

${\displaystyle (AB)'=A'+B'\,}$

Todas estas formas de representación son correctas, se utilizan de hecho, y pueden verse al consultar bibliografía. La utilización de una u otra notación no modifica el álgebra de Boole, solo su aspecto, y depende de la rama de las matemáticas o la tecnología en la que se esté utilizando para emplear una u otra notación.

Estructuras algebraicas que son álgebra de Boole

Hay numerosos casos de distintos análisis de estructuras algebraicas que corresponden al álgebra de Boole, aunque en apariencia son muy diferentes, su estructura es la misma. Vamos a ver algunos de ellos, con el propósito de hacer palpable las similitudes en la estructura y los distintos ámbitos de aplicación y distinta terminología para referirse a las operaciones o a las variables.

Lógica binaria

Una serie de temas, aparentemente tan distintos, tiene dos cosas en común, la lógica binaria basada en los ceros y los unos y el álgebra de Boole, posiblemente la forma más conocida de esta álgebra, que en ocasiones da lugar a la interpretación que el álgebra de Boole es la lógica binaria exclusivamente, así el conjunto ${\displaystyle {\mathfrak {B}}}$ en este caso está formado por dos elementos {0,1}, o {F, V}, o {no, sí}, dos valores contrapuestos, que son las dos posibles alternativas entre dos situaciones posibles, aquí, sin pérdida de la generalidad, tomaremos el conjunto: {0,1} como ya hemos dicho:

${\displaystyle {\mathfrak {B}}=\{0,1\}}$

Donde:

${\displaystyle \varnothing =0}$

${\displaystyle U=1\;}$

• La operación unaria interna, que llamaremos negación:

${\displaystyle {\begin{array}{c|c}a&{\bar {a}}\\\hline 0&1\\1&0\end{array}}}$

${\displaystyle {\begin{array}{rrcl}{\bar {}}:&{\mathfrak {B}}&\to &{\mathfrak {B}}\\&a&\to &b={\bar {a}}\end{array}}}$

La operación unaria interna negación, definimos una aplicación que a cada elemento a de {0,1}, le asigna un b de {0,1}.

${\displaystyle \forall a\in {\mathfrak {B}}\,:\quad \exists !b\in {\mathfrak {B}}\;/\quad b={\bar {a}}}$

Para todo elemento a en {0.1}, se cumple que existe un único b en {0,1}, tal que b es la negación de a. Como se ve en la tabla.

• La operación binaria interna, que llamaremos suma:

${\displaystyle {\begin{array}{c|cc}+&0&1\\\hline 0&0&1\\1&1&1\end{array}}}$

${\displaystyle {\begin{array}{rrcl}+:&{\mathfrak {B}}\times {\mathfrak {B}}&\to &{\mathfrak {B}}\\&(a,b)&\to &c=a+b\end{array}}}$

Con la operación suma definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.

${\displaystyle \forall (a,b)\in {\mathfrak {B}}\times {\mathfrak {B}}\,:\quad \exists !c\in {\mathfrak {B}}\;/\quad c=a+b}$

Para todo par ordenado (a,b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de sumar a con b.

• la operación binaria interna, que llamaremos producto:

${\displaystyle {\begin{array}{c|cc}\cdot &0&1\\\hline 0&0&0\\1&0&1\end{array}}}$

${\displaystyle {\begin{array}{rrcl}\cdot :&{\mathfrak {B}}\times {\mathfrak {B}}&\to &{\mathfrak {B}}\\&(a,b)&\to &c=a\cdot b\end{array}}}$

Con la operación producto definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.

${\displaystyle \forall (a,b)\in {\mathfrak {B}}\times {\mathfrak {B}}\,:\quad \exists !c\in {\mathfrak {B}}\;/\quad c=a\cdot b}$

Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado del producto a y b. Como se puede ver en la tabla.

Axiomas

Así ${\displaystyle (\{0,1\},{\bar {}},+,\cdot )}$ es un álgebra de Boole al cumplir los siguientes axiomas:

• 1a: La ley asociativa de la suma:

${\displaystyle \forall a,b,c\in \{0,1\}:\;(a+b)+c=a+(b+c)}$

• 1b: La ley asociativa del producto:

${\displaystyle \forall a,b,c\in \{0,1\}:\;(a\cdot b)\cdot c=a\cdot (b\cdot c)}$

• 2a: Existencia del elemento neutro para la suma:

${\displaystyle \forall a\in \{0,1\}:\;a+0=a}$

• 2b: Existencia del elemento neutro para el producto:

${\displaystyle \forall a\in \{0,1\}:\;a\cdot 1=a}$

• 3a: La ley conmutativa de la suma:

${\displaystyle \forall a,b\in \{0,1\}:\;a+b=b+a}$

• 3b: La ley conmutativa del producto:

${\displaystyle \forall a,b\in \{0,1\}:\;a\cdot b=b\cdot a}$

• 4a: Ley distributiva de la suma respecto al producto:

${\displaystyle \forall a,b,c\in \{0,1\}:\;a+(b\cdot c)=(a+b)\cdot (a+c)}$

• 4b: Ley distributiva del producto respecto a la suma:

${\displaystyle \forall a,b,c\in \{0,1\}:\;a\cdot (b+c)=(a\cdot b)+(a\cdot c)}$

• 5a: Existe elemento complementario para la suma:

${\displaystyle \forall a\in \{0,1\};\;\exists {\bar {a}}\in \{0,1\}:\;a+{\bar {a}}=1}$

• 5b: Existe elemento complementario para el producto:

${\displaystyle \forall a\in \{0,1\};\;\exists {\bar {a}}\in \{0,1\}:\;a\cdot {\bar {a}}=0}$

Luego ${\displaystyle (\{0,1\},{\bar {}},+,\cdot )}$ es álgebra de Boole.

Teoremas fundamentales

Partiendo de estos axiomas se puede demostrar los siguientes teoremas:

• 6a: Ley de idempotencia para la suma:

${\displaystyle \forall a\in \{0,1\}:\;a+a=a}$

• 6b: Ley de idempotencia para el producto:

${\displaystyle \forall a\in \{0,1\}:\;a\cdot a=a}$

• 7a: Ley de absorción para la suma:

${\displaystyle \forall a\in \{0,1\}:\;a+1=1}$

• 7b: Ley de absorción para el producto:

${\displaystyle \forall a\in \{0,1\}:\;a\cdot 0=0}$

• 8a: Ley de identidad para la suma:

${\displaystyle \forall a\in \{0,1\}:\;a+0=a}$

• 8b: Ley de identidad para el producto:

${\displaystyle \forall a\in \{0,1\}:\;a\cdot 1=a}$

• 9: Ley de involución:

${\displaystyle \forall a\in \{0,1\}:\;{\bar {\bar {a}}}=a}$

• 10: Ley del complemento:

${\displaystyle {\bar {1}}=0}$

${\displaystyle {\bar {0}}=1}$

• 11: Leyes de De Morgan:

${\displaystyle \forall a,b\in \{0,1\}:\;{\overline {a+b}}={\bar {a}}\cdot {\bar {b}}}$

${\displaystyle \forall a,b\in \{0,1\}:\;{\overline {a\cdot b}}={\bar {a}}+{\bar {b}}}$

Orden en el álgebra de Boole

Partiendo de ${\displaystyle (\{0,1\},{\bar {}},+,\cdot )}$ álgebra de Boole, dadas dos variables binarias: a, b, que cumplen alguna de estas condiciones:

${\displaystyle \left.{\begin{array}{l}a+b=b\\a\cdot b=a\\{\bar {a}}+b=1\\a\cdot {\bar {b}}=0\end{array}}\right\}\longrightarrow \quad a\leq b}$

entonces a es menor o igual que b. Dados los valores binarios 0 y 1, podemos ver:

1. ${\displaystyle 0+1=1}$
2. ${\displaystyle 0\cdot 1=0}$
3. ${\displaystyle {\bar {0}}+1=1}$
4. ${\displaystyle 0\cdot {\bar {1}}=0}$

Estas cuatro condiciones son equivalentes y el cumplimiento de una de ellas supone el cumplimiento de las otras, en este caso es sencillo comprobarlas todas. Luego podemos decir que 0 antecede a 1 y lo denotamos:

${\displaystyle 0\leq 1}$

Si además sabemos que 0 y 1 son valores distintos:

${\displaystyle \left.{\begin{array}{l}0\leq 1\\0\neq 1\end{array}}\right\}\longrightarrow \quad 0<1}$

El valor binario 0 es menor que el valor binario 1.

Operaciones en álgebra de Boole

El álgebra de Boole se basa en un conjunto en el que se han definidos tres operaciones internas: una unaria y dos binarias, como ya hemos visto, siendo cómoda esta definición. Estrictamente hablando solo son necesarias dos, la unaria y una de las binarias, así, por ejemplo, en la lógica binaria con la negación y el producto podemos definir la suma.

Con la ley de De Morgan:

${\displaystyle \forall a,b\in \{0,1\}:\;{\overline {a+b}}={\bar {a}}\cdot {\bar {b}}\longrightarrow \quad a+b={\overline {{\bar {a}}\cdot {\bar {b}}}}}$

Esta expresión resulta más compleja, pero partiendo de la negación y el producto binarios define la suma binaria.

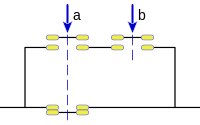
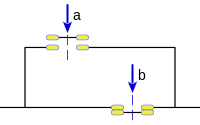
En la imagen de la derecha podemos ver un circuito en paralelo de dos pulsadores a y b, que corresponde a la suma binaria de a y b, y su equivalente en un circuito en serie de a y b, los dos dan como resultado la misma tabla de verdad, y por tanto son equivalentes, lo artificioso el circuito serie para obtener el mismo resultado que en un circuito paralelo deja ver lo conveniente de considerar esa función, la posibilidad de obtener la suma de dos variables binarias mediante la negación y el producto señalan que, de forma primaria, el álgebra de Boole se basa solo en dos operaciones, y que cualquier expresión en la que intervenga la suma puede transformarse en otra equivalente en la que solo intervienen la negación y el producto.

En el caso de la teoría de conjuntos con el complemento y la intersección podemos definir la unión:

${\displaystyle {(A\cup B)}^{C}={A}^{C}\cap {B}^{C}\longrightarrow \quad A\cup B={({A}^{C}\cap {B}^{C})}^{C}}$

De una forma similar al álgebra binaria, o cualquier otra álgebra de Boole, La definición del álgebra con solo dos operaciones complica las expresiones, pero permite determinar ciertas relaciones muy útiles, así como otras operaciones distintas.

En el álgebra de Boole definido en un conjunto ${\displaystyle {\mathfrak {B}}}$ las operaciones son internas, dado que parte de elemento de ${\displaystyle {\mathfrak {B}}}$, para obtener un resultado en ${\displaystyle {\mathfrak {B}}}$.

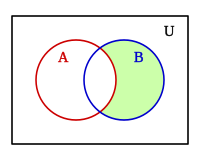
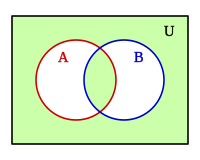
Sin perdida de la generalidad, y dado los distintos formas que puede adoptar el álgebra de Boole consideraremos la lógica proposicional con las proposiciones: a, c, b, etc. Que pueden tomar los valores verdadero: V o falso: F. Y las conectivas lógicas sobre esas proposiciones que dan como resultado otras proposiciones lógicas, cada proposición: a, b, c, etc. Define un conjunto A, B, C, etc. Que podemos representar de forma gráfica en un diagrama de Venn.

Operaciones nularias

Una operación nularia es la que devuelve un valor sin necesidad de argumentos, podemos ver tautología y contradicción

${\displaystyle {\begin{array}{|c||c|}\hline &\top \\\hline \hline &V\\\hline \end{array}}}$

La tautología presenta el valor verdadero sin necesidad de argumentos o independientemente de las variables sobre la que se calcule. En teoría de conjuntos corresponde al conjunto universal.

En lógica proposicional corresponde al valor: verdadero:

${\displaystyle {\begin{array}{ccll}\top :&\varnothing &\longrightarrow &\mathbb {U} \\&()&\longrightarrow &a=\top ()\equiv a=V\end{array}}}$

En un circuito de conmutación corresponde a una conexión fija o puente cerrado.

${\displaystyle {\begin{array}{|c||c|}\hline &\bot \\\hline \hline &F\\\hline \end{array}}}$

La contradicción, por el contrario, presenta siempre el valor falso, sin necesitar argumentos o independientemente de los argumentos presentados. En teoría de conjuntos corresponde al conjunto vacío.

En lógica proposicional corresponde al valor: falso:

${\displaystyle {\begin{array}{ccll}\bot :&\varnothing &\longrightarrow &\mathbb {U} \\&()&\longrightarrow &a=\bot ()\equiv a=F\end{array}}}$

En un circuito de conmutación, corresponde a la no conexión o puente abierto.

Operaciones unarias

Una operación unaria es la que solo necesita un argumento para presentar un resultado, podemos ver dos operaciones unarias: identidad y negación.

${\displaystyle {\begin{array}{|c||c|}\hline a&a\\\hline \hline V&V\\F&F\\\hline \end{array}}}$

La operación identidad de una afirmación presenta el valor de la variación.

${\displaystyle {\begin{array}{ccll}id:&\mathbb {U} &\longrightarrow &\mathbb {U} \\&a&\longrightarrow &b=id(a)\equiv b=a\end{array}}}$

Esta operación se puede hacer con el dispositivo electrónico amplificador buffer.

En un circuito de conmutación corresponde a un interruptor normalmente abierto: Interruptor NA.

${\displaystyle {\begin{array}{|c||c|}\hline a&\lnot a\\\hline \hline V&F\\F&V\\\hline \end{array}}}$

La operación negación lógica de una variable presenta el valor contrario del argumento, o los casos contrarios de los recogidos en el argumento.

${\displaystyle {\begin{array}{ccll}\lnot :&\mathbb {U} &\longrightarrow &\mathbb {U} \\&a&\longrightarrow &b=\lnot (a)\equiv b=\lnot a\end{array}}}$

Esta operación se hace con la Puerta NOT.

En un circuito de conmutación corresponde a un interruptor normalmente cerrado: Interruptor NC.

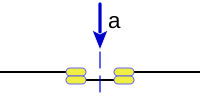Operaciones binarias

La operación binaria es la que necesita dos argumentos, de hecho es la forma más generalizada de operación, normalmente cuando nos referimos a operaciones, nos referimos a operaciones binarias, en el álgebra de Boole podemos ver las siguientes operaciones binarias:

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\land b\\\hline \hline V&V&V\\V&F&F\\F&V&F\\F&F&F\\\hline \end{array}}}$

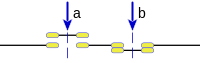
• La Conjunción lógica presenta resultado verdadero solo cuando sus dos argumentos son verdaderos.

${\displaystyle {\begin{array}{ccll}\land :&\mathbb {U} \times \mathbb {U} &\longrightarrow &\mathbb {U} \\&(a,b)&\longrightarrow &c=\land (a,b)\equiv c=a\land b\end{array}}}$

Normalmente representado:

${\displaystyle a\land b}$

La conjunción lógica de proposiciones es equivalente a la intersección de conjuntos en teoría de conjuntos, o a la puerta lógica AND:

en circuitos de conmutación seria un circuito en serie de interruptores.

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\uparrow b\\\hline \hline V&V&F\\V&F&V\\F&V&V\\F&F&V\\\hline \end{array}}}$

• La Conjunción opuesta presenta resultado verdadero en todos los casos excepto cuando sus dos argumentos son verdaderos. Esta operación es la negación de la conjunción.

${\displaystyle a\uparrow b\;=\;\lnot (a\land b)\;=\;\lnot a\lor \lnot b}$

La conjunción lógica de proposiciones es equivalente a la puerta lógica NAND.

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\lor b\\\hline \hline V&V&V\\V&F&V\\F&V&V\\F&F&F\\\hline \end{array}}}$

• La Disyunción lógica acepta dos argumentos presentando como resultado verdadero si uno u otro de los argumentos es verdadero.

La disyunción puede expresarse:

${\displaystyle a\lor b\;=\;\lnot (\lnot a\land \lnot b)}$

La operación disyunción lógica de proposiciones, es equivalente a la unión de conjuntos en teoría de conjuntos, a la puerta lógica OR:

y al circuito en paralelo en circuitos de conmutación

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\downarrow b\\\hline \hline V&V&F\\V&F&F\\F&V&F\\F&F&V\\\hline \end{array}}}$

• La Disyunción opuesta presenta resultado verdadero solo cuando sus dos argumentos son falsos. Esta operación es la negación de la disyunción.

${\displaystyle a\downarrow b\;=\;\lnot (a\lor b)\;=\;\lnot a\land \lnot b}$

La negación conjunta de proposiciones es equivalente a la puerta lógica NOR.

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\to b\\\hline \hline V&V&V\\V&F&F\\F&V&V\\F&F&V\\\hline \end{array}}}$

• La Implicación presenta resultado falso si el primer argumento es verdadero y el segundo falso, en el resto de los casos presenta resultado verdadero, esta operación no es conmutativa y puede expresarse:

${\displaystyle a\to b\;=\;\lnot a\lor b\;=\;(a\land b)\lor \lnot a}$

A esta operación también se llama implicación: a implica b:

si a es verdadero b es verdadero.

si a es falso y b es verdadero, la implicación es falsa.

si a es falsa, la implicación es verdadera independientemente el valor de b.

A esta operación le corresponde un conjunto de puertas lógicas complejas:

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\nrightarrow b\\\hline \hline V&V&F\\V&F&V\\F&V&F\\F&F&F\\\hline \end{array}}}$

• La Adjunción lógica presenta resultado verdadero si el primer argumento es verdadero y el segundo falso, en el resto de los casos presenta resultado falso, esta operación no es conmutativa y es la negación de la condicional material, también suele llamarse diferencia de a y b, puede expresarse:

${\displaystyle a\nrightarrow b\;=\;\lnot (a\to b)\;=\;a\land \lnot b\;=\;a-b}$

A esta operación le corresponde un conjunto de puertas lógicas complejas:

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\leftarrow b\\\hline \hline V&V&V\\V&F&V\\F&V&F\\F&F&V\\\hline \end{array}}}$

• La Implicación opuesta es la operación que presenta resultado falso si el primer argumento es falso y el segundo verdadero, en el resto de los casos presenta resultado verdadero, esta operación no es conmutativa y es el resultado de permutar a y b en la condicional material, puede expresarse:

${\displaystyle a\leftarrow b\;=\;a\lor \lnot b}$

A esta operación le corresponde un conjunto de puertas lógicas complejas:

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\nleftarrow b\\\hline \hline V&V&F\\V&F&F\\F&V&V\\F&F&F\\\hline \end{array}}}$

• La Adjunción opuesta presenta resultado verdadero si el primer argumento es falso y el segundo verdadero, en el resto de los casos presenta resultado falso, esta operación no es conmutativa y es la negación de la condicional inverso, también suele llamarse diferencia: b - a, puede expresarse:

${\displaystyle a\nleftarrow b\;=\;\lnot (a\leftarrow b)\;=\;\lnot a\land b\;=\;b-a}$

A esta operación le corresponde un conjunto de puertas lógicas complejas:

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\leftrightarrow b\\\hline \hline V&V&V\\V&F&F\\F&V&F\\F&F&V\\\hline \end{array}}}$

• La Bicondicional presenta resultado verdadero si los dos argumentos son iguales, esto es: si a y b son verdaderos o si a y b son falsos.

${\displaystyle a\leftrightarrow b\;=\;(a\land b)\lor (\lnot a\land \lnot b)}$

Le corresponde la Puerta XNOR.

---

${\displaystyle {\begin{array}{|c|c||c|}\hline a&b&a\nleftrightarrow b\\\hline \hline V&V&F\\V&F&V\\F&V&V\\F&F&F\\\hline \end{array}}}$

• La Disyunción exclusiva presenta resultado verdadero si los dos argumentos son dispares, esto es si de los dos argumentos uno es verdadero y otro falso, es la negación de la bicondicional:

${\displaystyle a\nleftrightarrow b\;=\;\lnot (a\leftrightarrow b)\;=\;(a\land \lnot b)\lor (\lnot a\land b)}$

Esta operación también se llama o exclusivo, uno o el otro pero no los dos, le corresponde la puerta lógica: XOR.

Fórmula de Boole bien formada

Partiendo de un conjunto: ${\displaystyle {\mathfrak {B}}}$ y donde a, b, c, d, ... son variables o constantes que pueden tomar valores del conjunto ${\displaystyle {\mathfrak {B}}}$, donde se han definido las siguientes operaciones internas:

${\displaystyle {\begin{array}{rrcl}\sim :&{\mathfrak {B}}&\to &{\mathfrak {B}}\\&a&\to &b=\sim a\end{array}}}$

${\displaystyle {\begin{array}{rrcl}\oplus :&{\mathfrak {B}}\times {\mathfrak {B}}&\to &{\mathfrak {B}}\\&(a,b)&\to &c=a\oplus b\end{array}}}$

${\displaystyle {\begin{array}{rrcl}\odot :&{\mathfrak {B}}\times {\mathfrak {B}}&\to &{\mathfrak {B}}\\&(a,b)&\to &c=a\odot b\end{array}}}$

podemos decir que son fórmulas bien formadas: fbf:

1: Una variable o constante:

${\displaystyle a\;}$

2: La negación de una variable o constante:

${\displaystyle \sim a\;}$

3: La operación binaria entre dos variables o constantes:

${\displaystyle a\oplus b\;}$

4: El resultado de sustituir en una fórmula bien formada, una variable o constante por una fórmula bien formada:

${\displaystyle \left.{\begin{array}{l}a\oplus b\\a=c\odot d\end{array}}\right\}\longrightarrow \quad (c\odot d)\oplus b}$

La aplicación repetida de estos criterios dará siempre una fórmula bien formada.

ejemplo:

${\displaystyle \left.{\begin{array}{l}\left.{\begin{array}{l}\sim a\\a=b\odot c\end{array}}\right\}\longrightarrow \quad \sim (b\odot c)\\\;c=d\oplus e\end{array}}\right\}\longrightarrow \quad \sim (b\odot (d\oplus e))}$

Se podrán emplear tantos paréntesis como sean necesarios para evitar ambigüedades, evitando siempre la utilización superflua de paréntesis.

Jerarquía de los operadores

Al evaluar una expresión booleana, deben realizarse las operaciones de acuerdo con su nivel jerárquico, realizando primero la de mayor jerarquía. Si existen paréntesis, deben resolverse primero los más internos y trabajar hacia fuera. En ausencia de paréntesis, la jerarquía de las operaciones es, de mayor a menor, la siguiente:

1. ${\displaystyle \sim }$
2. ${\displaystyle \odot }$
3. ${\displaystyle \oplus }$

Si se tienen varias operaciones con la misma jerarquía, éstas pueden ser evaluadas de derecha a izquierda o de izquierda a derecha, el resultado será el mismo.

Como ejemplo, considérese la evaluación de las siguientes expresiones booleanas:

${\displaystyle \sim a\odot b\quad \longleftrightarrow \quad (\sim a)\odot b}$

${\displaystyle a\oplus b\odot c\quad \longleftrightarrow \quad a\oplus (b\odot c)}$

${\displaystyle a\oplus b\oplus c\quad \longleftrightarrow \quad (a\oplus b)\oplus c\quad \longleftrightarrow \quad a\oplus (b\oplus c)}$